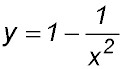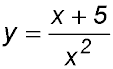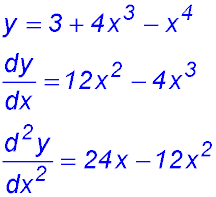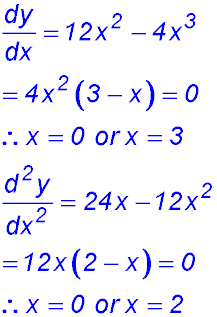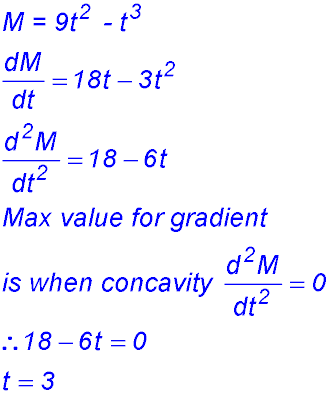Dr. J's Maths.com
Where the techniques of Maths
are explained in simple terms.

Calculus - Differentiation - Applications of Calculus.
2nd derivative - Concavity -Test Yourself 1 - Solutions.


 

Now for the solutions:

Find the concavity. 1. Find the concavity function for the curve given by y = x3(x - 2). 2. Determine the value of the concavity for the function

y = (1 - 3x)3

at x = 1 and interpret its sign graphically.
Finding points of concavity change. 3. Find the point(s) on the curve

y = x3 - 3x2 - 9x + 11

where the concavity changes sign.

 4. Find the point(s) on the curve

y = 12x3 -3x4 + 11

where the concavity changes sign.
 

5. Find the regions on the curve

y = x3 - x2 - 4x - 3 where the curve is

(i) concave up;

(ii) concave down.

6. Find the regions on the curve y = 27x - x3

where the the curve is

(i) concave up;

(ii) concave down.
Interpreting concavity of a curve. 7. Show that the curve

is always concave down.

8. Show that the curve

is always concave up when x > 0.
 

9. (i) the first two derivatives:

(ii)

(iii) At x = 3, there appears to be a stationary point. Substituting x = 3 into the 2nd derivative gives a value of -36 which implies there is a maximum point at x = 3.

At x = 2 there is a point of inflection. Testing:

x 1 2 3
f ''(x) 12 0 -36

Change of sign ∴ a change in concavity. POI.

At x = 0, both derivatives = 0. Hence the gradient and the inflection = 0. ∴ possible horizontal point of inflection.

Checking for a gradient change about x = 0:

x -1 0 1
f '(x) 16 0 8

There is no gradient change from positive.

∴ horizontal POI at x = 0.

(iv)

10. For the curve

y = 2x4 - 4x3 + 2x2 + 10:

(i) find the first two derivatives;

(ii) find the x values which solve each of the equations f '(x) = 0 and f "(x) = 0;

(iii) comment on the shape of the curve at the five x values you have found.
1st and 2nd derivative combinations. 11. The first and second derivative functions of a curve are:

f '(x) = x(x - 3)(x + 5)

f "(x) = 3x2 + 4x -15

(i) Find the x values for which the gradient of the original curve is zero.

(ii) Find the x values for which the curve is concave down.

 12. If g(x) = x + 2x2, solve the equation

g '(a) = g "(a).
  13. Find the values for a, b and c if the curve
y = x3 + ax2 - bx + c has a
  • intercept at x = 1;
  • a stationary point at x = -2 and
  • a point of inflection at x = -0.5
 14. Given the equation y = x3 - x2 - x + 6,

find the x values where the curve is both decreasing and concave up.
  15. The graph of f(x) = 7 + 5x - x2 - x3 is defined in the domain [-3, 3].

(i) Find the coordinates of the stationary points and determine their nature.

(ii) Find the coordinates of any points of inflexion.

(iii) Hence sketch the curve y = f(x) in the given domain.

(iv) For what values of x is the curve concave down?

Answer.(i) Maximum at (1, 10) and
minimum at (-5/3, 14/27).
(ii) POI at (-1/3, 148/27).
(iv) Concave up for (-3, -1/3).		 16. (i)

(ii) the two stationary points:

 

(iii) Sketch the curve.

(iv) For what values of x is the curve concave up?

Answer.(ii) Min at (2, 4)
Max at (-2, -4),
(iv) Concave up for x > 0.
  17. Consider the function
f(x) = x3 - x2 - 5x + 1.

(i) Find the coordinates of the stationary points of the curve y = f(x) and determine their nature.

(ii) Find any points of inflexion.

(iii) Sketch the curve y = f(x) for
[-2, 2] clearly indicating the endpoints. You do not need to find the x-intercepts.

(iv) For what values of x is the curve y = f(x) decreasing but concave up?

Answer.(i) Max at (-1, 4)
Min at (5/3, -5.48).
(ii) POI at (1/3, 0.74).
(iv) [1/3, 2].		 18. For the function f(x) = 8x3 - 8x2:

(i) Find the stationary points and determine their nature.

(ii) Find the co-ordinates of any points of inflexion.

(iii) Sketch the graph of the function y = f(x) showing stationary points, points of inflexion and x and y intercepts.

(iv) For what values of x is the curve concave down and decreasing?

Answer.(i) Max at (0, 0)
Min at (2/3, -1.185).
(ii) POI at (1/3, -0.59).
(iv) 0 < x < 1/3.
Maximum gradient.

19. Find the maximum gradient of the curve

y = x3 - 6x2 + 5

20.

Could use the 1st derivative and draw the parabola. Could also use a table to prove zero concavity.
 

20.

21.

 

22. Prove that the graph of

y = ax3 + bx2 + cx + d
has two distinct turning points if b2 > 3ac.

Find the values of a, b, c and d for which the graph of this form has turning points at (0.5, 1) and at (1.5, -1)

23.